Noviembre

01 DE NOVIEMBRE DEL 2016

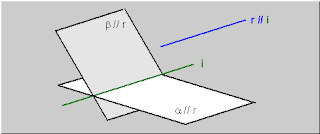
LA RECTA EN R3

La recta en R3 tiene varios elementos; puntos  M₀ y los vectores hacia este punto r₀  finalmente formado por un vector director de la recta L denotado por a= (l, m, n)

·         Ecuación vectorial de la recta

·         Ecuaciones  paramétricas

·         Ecuaciones simétricas o cartesianas de la recta

Observaciones:

v   La recta es un caso particular de una CURVA  ALABEADA

v  Si puede  proyectar una recta sobre cualquier plano coordenado

ECUACION DE LA RECTA DADOS DOS PUNTOS

Tal como se menciona para hallarla se requiere de la presencia de dos puntos y se obtiene la ecuación siguiente en R2

En R3 se trata de la misma ecuación incluida una variable más

08 DE NOVIEMBRE DEL 2016

RECTA DETERMINADA POR DOS PLANOS

Se parte como premisas de las ecuaciones de los dos planos, sabiendo que toda recta corta con los planos coordenados en algún punto

La ecuación obtenida es la siguiente, siendo (a) el vector director de la recta L

HAZ DE PLANOS

Conjunto infinito de planos que pasa por una misma recta, para esta recta  se parte de dos ecuaciones de los planos  y se obtiene la ecuación del haz de planos

·         Ecuación del haz de planos

DISTANCIA DE UN  PUNTO A LA RECTA

Como premisas el punto y la  ecuación de la recta y mediante definiciones de producto punto, cruz se obtiene la fórmula para simplificar el cálculo para hallar esta distancia:

ECUACIÓN VECTORIAL DE LA ESFERA

A partir de la esfera, conociendo su centro y su radio se puede construir la ecuación  vectorial de la esfera:

 

SUPERFICIES DE SEGUNDO ORDEN (CUADRÁTICAS)

Se llama así a las superficies en el espacio que vienen dadas por ecuaciones de 2do grado

Ax^2 + By^2 + Cz^2 + 2Dxy +2Exz +2Fyz + 2Gx + 2Hy + 2Kz + 1 = 0

11 DE NOVIEMBRE DEL 2016

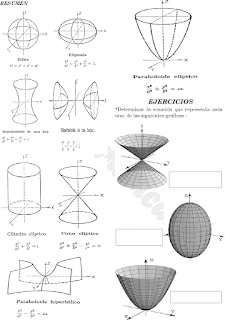
Para determinar correctamente que superficie cuadrática corresponde a las diferentes ecuaciones dadas se  debe seguir el siguiente procedimiento:

1.      Intersección con los ejes coordenados

2.      Intersección con los planos coordenados

3.      Intersección con los planos paralelos a los planos coordenados

4.      Bosquejo de la gráfica de la superficie

ELIPSOIDE

CASOS PARTICULARES

Ø  Si a ≠ b ≠ c elipsoide escaleno

Ø  Si a = b ≠ c elipsoide de revolución

Ø  Si a = b = c superficies esféricas 

HIPERBOLOIDE DE UNA HOJA

HIPERBOLOIDE DE DOS HOJAS

CONO DE SEGUNDO ORDEN

PARABOLOIDE

PARABOLOIDE HIPERBOLICO

15 DE NOVIEMBRE DEL 2016

FUNCIONES VECTORIALES

Se llama función vectorial  de la variable real t, a toda función  Ḟ (t) de I en Rⁿ, donde  t pertenece  “I” y a los R.

t= F (t) = (f1 (t), f2 (t)…. fn (t))

Donde f (t)    funciones escalares rectas reales de I en R

Ø  Si n=2 entonces [a , b] ∈ R

La trayectoria es una curva en el plano  o curva plana

Ø  Si n = 3, entonces  

OPERACIONES CON FUNCIONES VECTORIALES

Dadas dos funciones vectoriales se pueden realizar distintas  operaciones similares a las operaciones entre vectores como:

18 DE NOVIEMBRE DEL 2016

LIMITES CONTINUIDAD Y DERIVACIÓN

LIMITES

"El límite de f(x) cuando x tiende a x0 es igual a L si y sólo si para todo número real ε mayor que cero existe un número real δ mayor que cero tal que si la distancia entre x y x0 es menor que δ, entonces la distancia entre la imagen de x y L es menor que ε".

Esta definición, se puede escribir utilizando términos matemáticos y de manera compacta:

Se escribe:

Lim _t—t0 f (t) = A

Si A vector = (a1, a2,……a_n) se prueba que: lim _t—& f_i (t) = a_i

Ɐ _i = 1, 2,3…..n

OBSERVACION:

Dada la función F  de I en R^n, donde F (t)= (f1 (t), f2 (t)….fn (t)); si una de ellas no tiene límite no existe límite de la función

CONTINUIDAD

Sea F de I a Rⁿ y sea t₀ pertenece a I se dice que F (t) es continua en t=to, si:

Lim _t—t0 F (t) = F (to)

OBSERVACION:

Si F de I en  Rⁿ, donde: F (t)= (f1 (t), f2 (t)….fn (t)), es continua en to, entonces

Lim _t—t0 F (t) = F (to) ↔ lim _t—t0 f_i (t) = f_i (to)              i= 1, 2, 3…..n

DERIVACIÓN

Dada F de I a Rⁿ, I pertenece a R y sea to pertenece a I, se dice que: F (t) es derivable en to si existe:

F (to) e un vector tangente a la curva en el punto F (to)

OBSERVACIONES;

Una función vectorial es derivable si cada una de sus componentes lo es.

Si n=3 → F: I € R³

t → F (t)= (f1 (t), f2 (t), f3 (t)); entonces

F’ (t) = (f1’ (t), f2’ (t), f3’ (t))

La derivada también se escribe así:

Las propiedades de la derivación de funciones son las mismas de la derivación de escalares y funciones reales de una variable

INTEGRACIÓN

PROPIEDADES:

22 DE NOVIEMBRE DEL 2016

VELOCIDAD Y ACELERACIÓN

Si F (t) de I en Rⁿ representa la función de posición de un móvil en el instante “t”, entones:

        i.            F’ (t) = V’ (t) : velocidad del móvil  |F’ (t)| = |V’ (t)| rapidez

      ii.             V (t) =|V (t)|

    iii.            Fⁿ (t) = A (t) :  aceleración del móvil

A (t) = V’ (t), entonces si

F (t) = (f1 (t), f2 (t), f3 (t))

V (t) = (f1’ (t), f2’ (t), f3’ (t))

A (t) = (f1’’ (t), f2’’ (t), f3’’ (t))

VECTORES TANGENTE UNITARIO  Y NORMAL PRINCIPAL

El vector tangente unitario se denota por  T (t); es el vector de la derivada de F divido para su módulo

El módulo de T (t) es igual a 1, entonces  F (t) y f’ (t) son ortogonales entre sí, por lo tanto, se define el vector normal principal

VECTOR BINOMIAL

El vector binomial  es el vector definido por:

B (t) = T (t)* N (t): es decir el producto cruz entre el vector tangente y el vector normal.

PLANO OSCULADOR

Si n= 3

El plano osculador, pasa por el punto F (t) y esta generado por T (t) y N (t), tangente y normal. Es l plano que mejor se ajusta  a la curva en una velocidad de F

n= (Bx, By, Bz);  p (xo, yo, zo)

Bx (x- xo) +By (y- yo) +Bz (z- zo) = 0

 

PLANO NORMAL

Se forma entre el vector  normal y binomial

T = (Tx, Ty, Tz);  p (x0, y0, z0)

Tx (x- xo) +Ty (y- yo) + Tz (z- zo) = 0

PLANO RECTIFICANTE

Se forma entre el actor tangente y el binomial

N= (Nx, Ny, Nz)    p (xo, yo, zo)

Nx (x- xo) + Ny (y- yo) + Nz (z- zo)

RECTA TANGENTE

La recta tangente es la recta que pasa por el vector tangente

a= T (t) = (Tx, Ty, Tz)

r= ro + t (Tx, Ty, Tz)

x= xo + tTx

y= yo + tTy

z= zo + tTz

RECTA NORMAL PRINCIPAL

La recta normal principal es la recta que pasa sobre el vector normal

a= N (t) = (Nx, Ny, Nz)

r= ro + t (Nx, Ny, Nz)

x= xo + tNx

y= yo + tNy

z= zo + tNz

RECTA BINOMIA

La recta que pasa por el vector binomial

a= B (t) = (Bx, By, Bz)

r= ro + t (Bx, By, Bz)

x= xo + tBx

y= yo + tBy

z= zo + tBz

25 DE NOVIEMBRE DEL 2016                         

VECTOR CURVATURA

Curvatura

La curvatura es una medida del cambio de dirección del vector tangente a una curva, cuanto más rápido cambia éste a medida que nos desplazamos a lo largo de la curva, se dice que es más grande la curvatura. Para una curva parametrizada cualquiera la curvatura es igual a:

${\displaystyle \chi (t)={\frac {\left\Vert \mathbf {r} '(t)\times \mathbf {r} ''(t)\right\|}{\left\Vert \mathbf {r} '(t)\right\|^{3}}}}$

Si la curva está parametrizada por el parámetro de longitud de arco, la anterior ecuación se reduce simplemente a:

${\displaystyle \chi (s)=\left\Vert \mathbf {\tilde {r}} ''(s)\right\|}$

 

La curvatura representa  la variacion del vector tangente respecto a la longitud de arco: se denomina vector curvatura al vector K= derivada de T con respecto a la derivada de s resoliendo se obtiene que el  vector curvatura es igual al módulo de  la derivada del vector tangente sobre la velocidad en funcion de t.

El inverso de la curvatura representa el radio de curvatura.

FUNCIONES REALES DE ARGUMENTO VECTORIAL

Sea D un subconjunto en Rn, se dice que f es una función real de argumento vectorial, si a cada elemento  x (x1, x2, x3, .... xn) le corresponde un único valor real de z

Se puede obtener el dominio y el rango de estas funciones

•   Para hallar el Dominio de la Función es recomendable analizarlo de tres maneras de manera analitica, gráfica y descritiva.

 

APLICACIÓN DE LAS FUNCIONES REALES

1. se aplican estas funciones para explicar fenomenos naturales como la Temperatura de la Tierra en función de la longitud y latitud
2. La Temperatura de una placa o lámina en funcion de la posición (x,y)
3. Las funciones de la densidad o distribución de masa f(x,y,z), que dependen de el largo, ancho y altura 
4. Incluso se puede expresar costos, la función  costos c=f (x,y) donde este dependerá de costos fijos y costos variables. 

CURVAS DE NIVEL

Se define como curvas de nivel a  el conjunto de  todos los puntos del plano donde f (x,y) tiene un valor constante, es decir f (x,y)=c, y se llama CURVA DE NIVEL DE F.

29 DE NOVIEMBRE DEL 2016

LIMITES  Y CONTINUIDAD

LIMITES
Para funciones de una sola variable, cuando dejamos que x se aproxime a a, sólo hay dos posibles direcciones de acercamiento, por la izquierda o por la derecha. Para funciones de dos variables, la situación no es tan sencilla, puesto que podemos dejar que (x, y) se aproxime a desde un número infinito de direcciones y de cualesquiera formas.
La definición anterior se refiere sólo a la distancia entre (x, y) y . No habla a la dirección de aproximación. Por eso, si el límite existe, entonces debe aproximarse a mismo límite, sin importar la forma en que (x, y) se aproxime a . Así pues, si podemos encontrar dos diferentes trayectorias de acercamiento a lo largo de las cuales tiene distintos límites, entonces se concluye que el límite no existe.
Si conforme a lo largo de una trayectoria y conforme a lo largo de una trayectoria ,donde , entonces el límite no existe.

CONTINUIDAD

 

Es similiar a la continuidad de las funciones de una variable:
se dice que es continua si:

• existe la funcion de f (xo, yo)
• si existe el limite de la función cuando tiende a (xo, yo)
• es continua si y solo si el limite es igual a la funcion evaluada en esos puntos